MECÂNCIA GENERALIZADA GRACELI DE INTERAÇÕES E TRANSFORMAÇÕES.

LEI -

TODA INTERAÇÃO LEVA A TRANSFORMAÇÕES, E VICE-VERSA.

INTERAÇÕES COMO E EM:

NAS INTERAÇÕES DAS FORÇAS FUNDAMENTIAS.

INTERAÇÕES DE SPIN - ÓRBITA.

ESTRUTURA - TEMPERATURA.

DISTRIBUIÇÃO ELETRÔNICA - NÍVEIS DE ENERGIA - BANDAS.

ELÉTRONS - FÓNOS.

ELÉTRONS - ELÉTRONS.

ESTADO QUÂNTICO - NÚMERO QUÃNTICO.

ENTROPIA -TEMPERATURA - MOVIMENTO BROWNIANO - CAMINHOS DE PARTÍCIULAS.

CATEGORIA - DIMENSÕES - FENÔMENOS [NO SISTEMA SDCTIE GRACELI].

ENTROPIA - ENTALPIA. ETC.

VEJAMOS AS INTERAÇÕES DE CAMPOS.

E EM RELAÇÃO AO SISTEMA DE MECÂNICA GENERALIZADO GRACELI.

eletromagnetismo quântico químico relativístico Graceli.

MECÂNICA DO SISTEMA DIMENSIONAL GRACELI.

ONDE A MAIORIA DOS FENÔMENOS FÍSICOS [EM TODAS AS ÁREAS] VARIAM CONFORME O SISTEMA DIMENSIONAL GRACELI.

SENDO ELE;

EQUAÇÃO GERAL DE GRACELI.[quantização de Graceli].

G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+].... .. =

G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+] $\lambda$ ψ ω ${\mathcal {T}}$ /c] = $\,N_{A}$ $\,M$ $\,z^{+}$ $\,z^{-}$ $\,e$ [/ $\,\epsilon _{o}$ ] / $\,r_{0}$ / = $\lambda$ ħω $q\ \$ [Ϡ ] [ξ ] [,ς] $g_{s}$ $\epsilon _{s}$ [ $\epsilon _{s}$ q G*] ${\begin{pmatrix}\psi _{0}\\\psi _{1}\end{pmatrix}}$ ψ μ / h/c ψ(x, t) $-i\hbar {\frac {\partial }{\partial x_{n}}}$ x t ]..

[ $\epsilon _{s}$ q [tG*] ==G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+].... ..

SISTEMA GRACELI DE:

TENSOR [tG+] GRACELI = IGFF + SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO E ESPECÍFICO NÍVEL DE ENERGIA., POTENCIAL DE ENERGIA, POTENCIAL QUÍMICO, SISTEMA GRACELI DO INFINITO DIMENSIONAL.

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

[ $\epsilon _{s}$ q [tG*] = energia quântica Graceli.

Força fundamental - INTERAÇÕES GRACELI IG =

IGFF = INTERAÇÕES GRACELI - Força fundamental.

T = TEMPERATURA.

PERMEABILIDADE MAGNÉTICA .

INTERAÇÃO SPINS ÓRBITA.

MOMENTUM MAGNÉTICO.

DISTRIBUIÇÃO ELETRÔNICA DOS ELEMENTOS QUÍMICOS.

NÍVEIS E SUBNIVEIS DE ENEREGIA.

BANDAS DE ENERGIAS.

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE. [1]

IGFF = FF / T . PM. ISO . MM. DEEQ. NE. BE./G ψ = E ψ =

\psi ^{*}

E [tG+].... .. [2]

Afinidade eletrônica (ou eletroafinidade), propriedade periódica, é a energia que um, e somente um átomo, em estado fundamental, no estado gasoso, liberta ao "ganhar" um elétron. Essa energia liberada é representada por um $\Delta H$ , a variação de entalpia do processo. Em se tratando de processos favoráveis - onde há tendência do átomo em ganhar elétron - o processo será mais exoenergético (Reação exotérmica), ou seja, haverá maior liberação de energia (o que implica um $\Delta H$ menor que zero). Segundo Mahan, Bruce M.; et. al.:

Em outras palavras, a afinidade eletrônica, A, é a quantidade mínima de energia necessária para remover um elétron de um ânion, para gerar um átomo neutro.".^[1]

Os processos favoráveis são aqueles em que o ganho de elétrons levará o átomo ao preenchimento da última camada eletrônica, ou ainda, levará o átomo a completar o octeto. A teoria do octeto proposta por Linus Pauling e amplamente conhecida em química diz que os átomos (representativos) mais estáveis são aqueles com oito elétrons na última camada, ou melhor, com a última camada completa, a exemplo os gases nobres.

Observando tais propriedades, desmente-se a ideia falsa de que os gases nobres (família 18) tem afinidade eletronica igual a zero. Tal conclusão equivocada pode vir da palavra "afinidade", sugerindo que átomos estáveis "não têm afinidade eletrônica". Na verdade, a afinidade eletrônica desses gases é menor em módulo, ou melhor, o processo é menos exotérmico para qualquer átomo gasoso com octeto completo. Observe que "afinidade eletrônica zero" representa um absurdo, uma vez que a admissão de um elétron por qualquer átomo necessariamente causa variação em sua energia.

A energia liberada é diretamente proporcional à energia potencial elétrica associada ao átomo e ao elétron admitido, e mostra-se inversamente proporcional ao raio atômico. Nas famílias da tabela periódica a afinidade eletrônica aumenta em módulo conforme diminui o número de camadas, ou seja, de baixo para cima. No período, a afinidade eletrônica aumenta, em módulo, conforme o número atômico aumenta: da esquerda para a direita. Os elementos que liberam maior energia ao ganhar um elétron são os halogênios, pois são os que estão mais próximos de atingir configuração eletrônica de um gás nobre. É digno de menção que o elemento 17 da tabela periódica, o cloro (Cl), é o elemento de maior afinidade eletrônica, liberando a maior das energias ao receber um elétron. ( $\Delta H=-349kJ/mol$ )

Afinidade eletrônica em matéria condensada

Principais energias em estrutura de bandas para sólidos cristalinos

Ao lidarmos com física do estado sólido e ao considerarmos técnicas de análise como a Espectroscopia de fotoelétrons excitados por raios X,^[2] a afinidade eletrônica é definida como a energia que seria liberada caso um elétron com energia de vácuo fosse introduzido na amostra, inicialmente neutra, ficando o mesmo por esta confinado. Sendo E_N^Total a energia total do sistema com N+1 elétrons, N na amostra, neutra e em seu equilíbrio termodinâmico, e E_N+1^Total a energia total do sistema em seu novo equilíbrio termodinâmico após a admissão do elétron, antes estático ao nível de vácuo, e após a liberação da energia envolvida no processo de admissão, temos:

χ = E_N^Total − E_N+1^{Total /}

/G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+].... ..

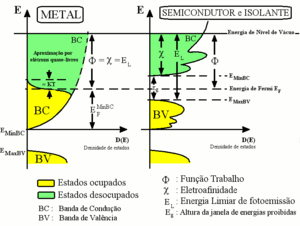
Um elétron, ao ser introduzido no sólido, deve ocupar, assumindo o equilíbrio termodinâmico, o primeiro estado disponível em energia, ou seja, o estado desocupado com menor energia na banda de condução. A eletroafinidade corresponde portanto à diferença de energias entre o nível de vácuo e a energia do primeiro estado livre, o menos energético dentro da banda de condução do sólido. No caso de metais, equipara-se à energia de Fermi. Em semicondutores, corresponde à diferença de energias entre o nível de vácuo e a energia mínima da banda de condução.

Relação fundamental em processos de fotoemissão

Equação fundamental

Conhecendo as energias anteriormente definidas estamos aptos a compreender a equação fundamental que descreve o processo de fotoemissão. Tal equação fundamenta-se no princípio da conservação da energia e considera que a energia total do sistema inicialmente em equilíbrio somada à energia do fóton incidente deve igualar-se à energia total do sistema em equilíbrio após o elétron ser ejetado, somada à energia necessária para se remover o elétron e à energia cinética deste elétron no vácuo:

$E_{N}^{total}+\hbar \omega =E_{N-1}^{total}+E_{cin}^{v}+\phi$ G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+].... ..

Reagrupando os termos acima teremos:

$E_{B}^{v}=\hbar \omega -(E_{cin}^{v}+\phi )$ G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+].... ..

A expressão acima corresponde à equação geral que governa o processo de fotoemissão com a referência de energia tomada necessariamente como a energia de vácuo uma vez que a energia cinética é definida no referencial da amostra e que a energia de ligação relatada também encontra-se referida à energia de vácuo. Alguns problemas práticos surgem ao se considerar um experimento real, entretanto. O primeiro refere-se ao fato que a energia de vácuo acima citada corresponde à energia de vácuo da amostra e não à energia de vácuo do dispositivo realmente responsável por medir a energia cinética dos elétrons, o analisador de elétrons. Isto se deve ao fato de que as funções trabalho do analisador e da amostra não são necessariamente iguais, e, considerando-se que ambos encontram-se eletricamente conectados, uma diferença de potencial de contato existe entre o analisador e a amostra.

A existência deste potencial de contato traz algumas implicações quanto à medida da energia cinética no analisador uma vez que a mesma implica a existência de um campo elétrico na região em vácuo compreendida entre a superfície da amostra e do analisador. Um elétron que, em relação ao nível de vácuo da amostra, possua uma energia cinética E_cin, seria percebido pelo analisador (em relação ao seu próprio nível de vácuo, portanto), como possuindo uma energia cinética dada por E_cin.medida = E_cin - e $\theta$ , onde -e é a carga do elétron e $\theta$ a diferença de potencial de contato entre a amostra e o analisador (e $\theta$ = $\Phi$ _amostra - $\Phi$ _analisador). O termo -e $\theta$ referese à energia ganha pelo elétron ao se mover da amostra até o analisador, estando a amostra em um potencial $\theta$ abaixo do potencial do analisador. A existência da diferença de potencial de contato não seria problema caso esta fosse constante, mas quando se considera que amostras diferentes em análise possuem, cada qual, uma função trabalho diferente, na maioria das vezes previamente desconhecida, um problema real existe.

O problema atrelado ao potencial de contato reside na escolha do referencial de energia e para solucioná-lo basta portanto redefinir a energia de referência para um nível de energia comum tanto à amostra como ao analisador. Este nível de referência é evidente: a energia de Fermi.

Considerando que a diferença entre o nível de vácuo da amostra e a energia de fermi da mesma é a sua função trabalho $\phi$ , a energia cinética E_CIN^F medida agora em relação ao nível de Fermi pode ser escrita como:

$E_{cin}^{F}=E_{cin}^{v}+\phi$ G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+].... ..

A equação fundamental em processos de fotoemissão torna-se então:

$E_{cin}^{F}=\hbar \omega -E_{B}^{F}$ G ψ = E ψ = IGFF $\psi ^{*}$ E [tG+].... ..

Nestas equações, tanto a energia de ligação E_B^F quanto a energia cinética E_cin^F referem-se agora à energia de Fermi, e usualmente costuma-se suprimir o "^F" nesta expressão. O termo energia cinética neste caso foge, é claro, dos rigores de sua definição clássica e as energias cinéticas e de ligação E_cin e E_B usualmente encontradas nas literatura encontram-se geralmente referidas à energia de fermi. Entretanto não são poucos os em que as mesmas encontram-se referidas ao nível de vácuo de forma que alguma atenção quanto a este ponto é sempre requerida ao se consultar as tais informações na literatura.

Espectros XPS são caracterizados por uma coletânea de pontos que apresentam flutuações características, o que implica, como já citado, em uma dispersão dos pontos experimentais ao redor dos valores ideais. A extração de informações dos espectros XPS exige em uma segunda etapa, mediante o uso de programa de processamento adequado a tal fim,^[4] o tratamento e o ajuste estatístico de uma função analítica sobre os dados de cada um dos picos de interesse do espectro, dos quais resultam informações confiáveis e relevantes sobre os valores das áreas, posições e larguras dos picos de interesse. A partir destes resultados é que informações física relevantes serão inferidas.

O primeiro procedimento na análise de um pico consiste na remoção dos “elétrons de fundo”, da base na qual este se assenta. O processo mais simples para a remoção dos elétrons de fundo consiste na extração de uma base linear sob o pico no espectro original, sendo aplicável sempre que a correta identificação das posições de pontos base do pico é possível. Na maioria dos casos que envolvem semicondutores, este é o caso.

O ajuste de uma função analítica pode ser feito empiricamente ou procurando-se razões experimentais e teóricas para escolher-se a função para o ajuste, e neste caso geralmente funções gaussianas, lorentzianas, ou em certos casos uma convolução das duas prestam-se bem ao serviço de ajuste aos dados experimentais. Em sua quase totalidade os ajustes destas funções a um mesmo pico fornecem resultados semelhantes para área, posição e largura de cada pico considerado, diferindo os resultados entre os ajustes por valores menores do que as incertezas nos resultados obtidos. Na figura vemos o ajuste do pico Ga3d para um espectro obtido de uma amostra de arseneto de gálio onde depositou-se uma pequena quantidade de césio na superfície. O ajuste é feito mediante uma função gaussiana, e o ajuste por lorentziana fornece resultados bem semelhantes.

A=A_{0}+{\frac {A_{1}}{w{\sqrt {\frac {\pi }{2}}}}}e^{-2({\frac {(x-x_{c})}{w}})^{2}}

uma função gaussiana típica usada na análise de espectros XPS: os parâmetros A₀, A₁, X_c e W são ajustados pelo programa de análise de forma que a curva ajuste-se da melhor forma possível aos dados experimentais.

Em metais a remoção de uma base linear pode não mostrar-se adequada devido a uma considerável elevação do patamar de elétrons secundários no lado do pico correspondente a menores energias cinéticas, sendo exemplo deste caso o pico Fe3p em espectros de Ferro (figura abaixo, espectro para 150A de Fe). Basicamente as estruturas são simétricas para materiais isolantes e semicondutores, mas não para metais, e um tratamento diferenciado para a remoção dos elétrons secundários faz-se então necessário. Nesse último caso uma função do tipo Doniach-Sunijic ou uma aproximação desta presta-se bem melhor à correta remoção da base formada pelos elétrons secundários e o uso de uma base linear é desencorajado.

Pesquisar este blog

MECÂNICA GENERALIZADA GRACELI - QUÂNTICA QUÍMICA RELATIVISTA [95]